學習記錄

今天是學習的第 22 天，主要學習了 BFS 的適用場景：

DFS 和 BFS 的適用場景

• 遞歸遍歷（DFS）：常用來窮舉所有路徑
• 層序遍歷（BFS）：常用來尋找最短路徑

為什麼 BFS 常用來尋找最短路徑

這邊以 LeetCode 第 111 題「二叉樹的最小深度」為例：

最小深度是從根節點到最近葉子節點（沒有子節點的節點）的最短路徑上的節點數量。

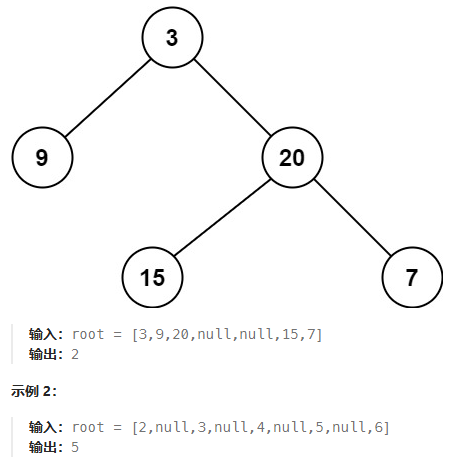
二叉樹的最小深度指的是「根節點到最近的葉節點的距離」，這邊先以 DFS 為例：

var minDepth = function(root) {
    if (root === null) {
        return 0;
    }
    
    // 記錄最小深度（根結點到最近的葉子節點的距離）
    let minDepthValue = Infinity;

    // 記錄當前遍歷到的節點深度
    let currentDepth = 0;

    const traverse = function(root) {
        if (root === null) {
            return;
        }

        // 前序位置進入節點時增加當前深度
        currentDepth++;

        // 如果當前節點是葉子節點，更新最小深度
        if (root.left === null && root.right === null) {
            minDepthValue = Math.min(minDepthValue, currentDepth);
        }

        traverse(root.left);
        traverse(root.right);

        // 後續位置離開節點時減少當前深度
        currentDepth--;
    };

    // 從根結點開始 DFS 遍歷
    traverse(root);
    return minDepthValue;
};

但 DFS 的寫法有個缺點：必須遍歷整棵樹才能找到最小深度，因為需要比較所有從根節點到葉子節點的路徑長度。

因此這裡可以利用 BFS 層序遍歷的特性，一旦遇到第一個葉子節點就能得到最小深度：

var minDepth = function(root) {
    if (root === null) return 0;
    let q = [root];

    // root 本身就是一層，depth 初始化為 1
    let depth = 1;

    while (q.length > 0) {
        let sz = q.length;
        // 遍歷當前層數的節點
        for (let i = 0; i < sz; i++) {
            let cur = q.shift();

            // 判斷是否到達葉子節點
            if (cur.left === null && cur.right === null)
                return depth;

            // 將下一層加入隊列
            if (cur.left !== null)
                q.push(cur.left);
            if (cur.right !== null)
                q.push(cur.right);
        }
        // 這裡增加深度
        depth++;
    }
    return depth;
};

由於 BFS 層序遍歷的特性，演算法可能不需要遍歷完所有節點就能提前結束。

學習總結

• 遞歸遍歷（DFS）：常用來窮舉所有路徑
• 層序遍歷（BFS）：常用來尋找最短路徑